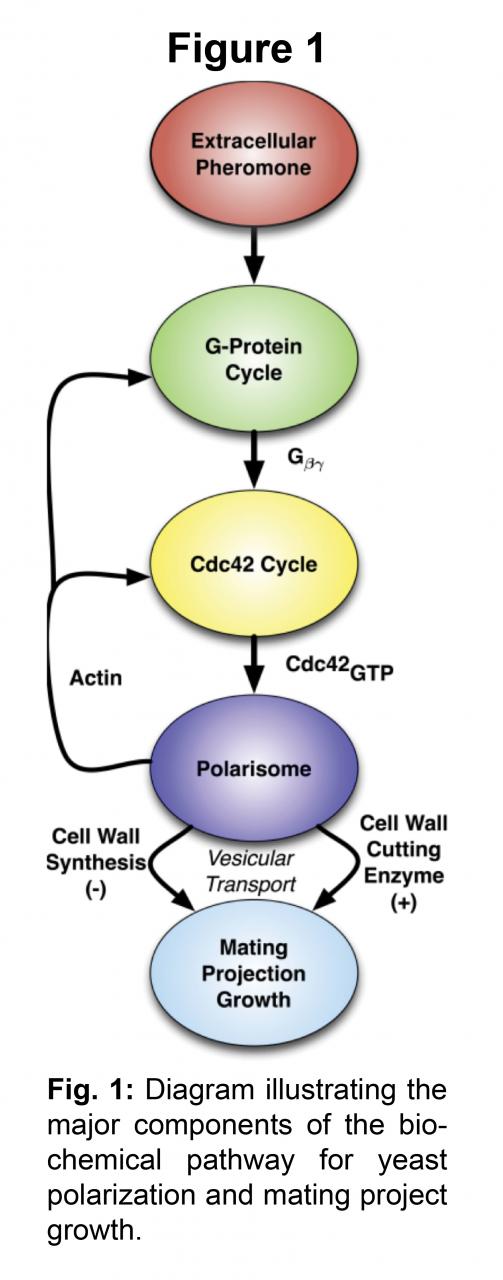
Cell polarization is a fundamental process that underlies many aspects of cell and developmental biology. In the polarization process, cellular components that were previously uniformly distributed become asymmetrically localized to create the complexity of form and function that is the hallmark of biological systems. One of the best-studied examples of cell polarization is the growth of the mating projection (shmoo) during yeast mating. Yeast cells localize specific proteins to the front of the cell in response to a spatial gradient of mating pheromone secreted by the partner. The spatial sensing and response exhibit remarkable sensitivity, dynamic range, and robustness.

Initially, using a combination of computational modeling and biological experiments, we closely examined an important prototype of cell polarity: the pheromone-induced formation of the yeast polarisome. We developed and investigated two mechanistic spatial models of polarisome formation, one deterministic and the other stochastic, and compared the contrasting predictions of these two models against experimental phenotypes of wild type and mutant cells. We found that the stochastic model can more robustly reproduce fundamental characteristics observed in wild-type cells, and demonstrated that higher levels of stochastic noise result in increased robustness. Our findings elucidate the intricate role of spatial stochastic effects in cell polarity, giving support to a cellular model where noise and spatial heterogeneity combine to achieve robust biological function [1].

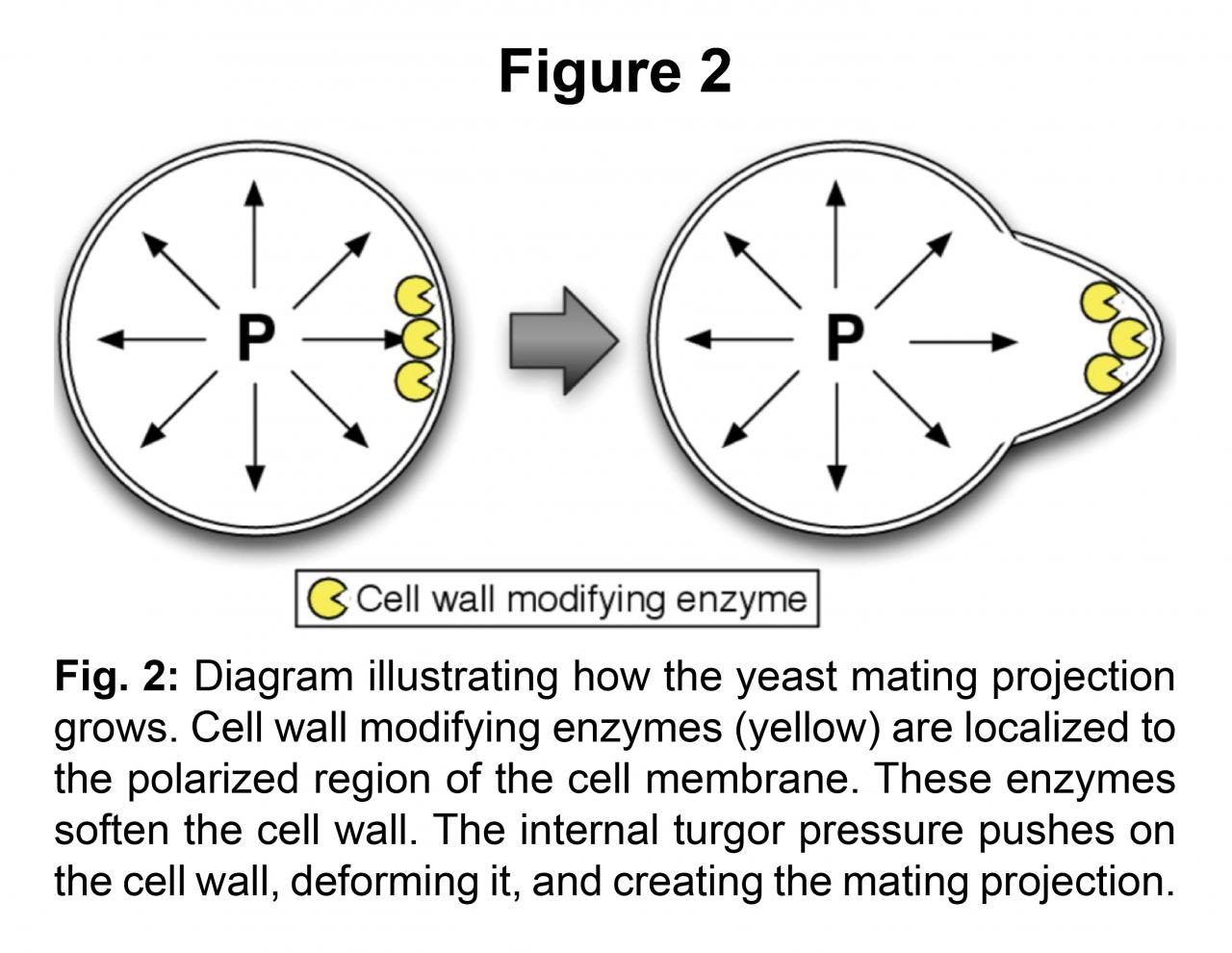
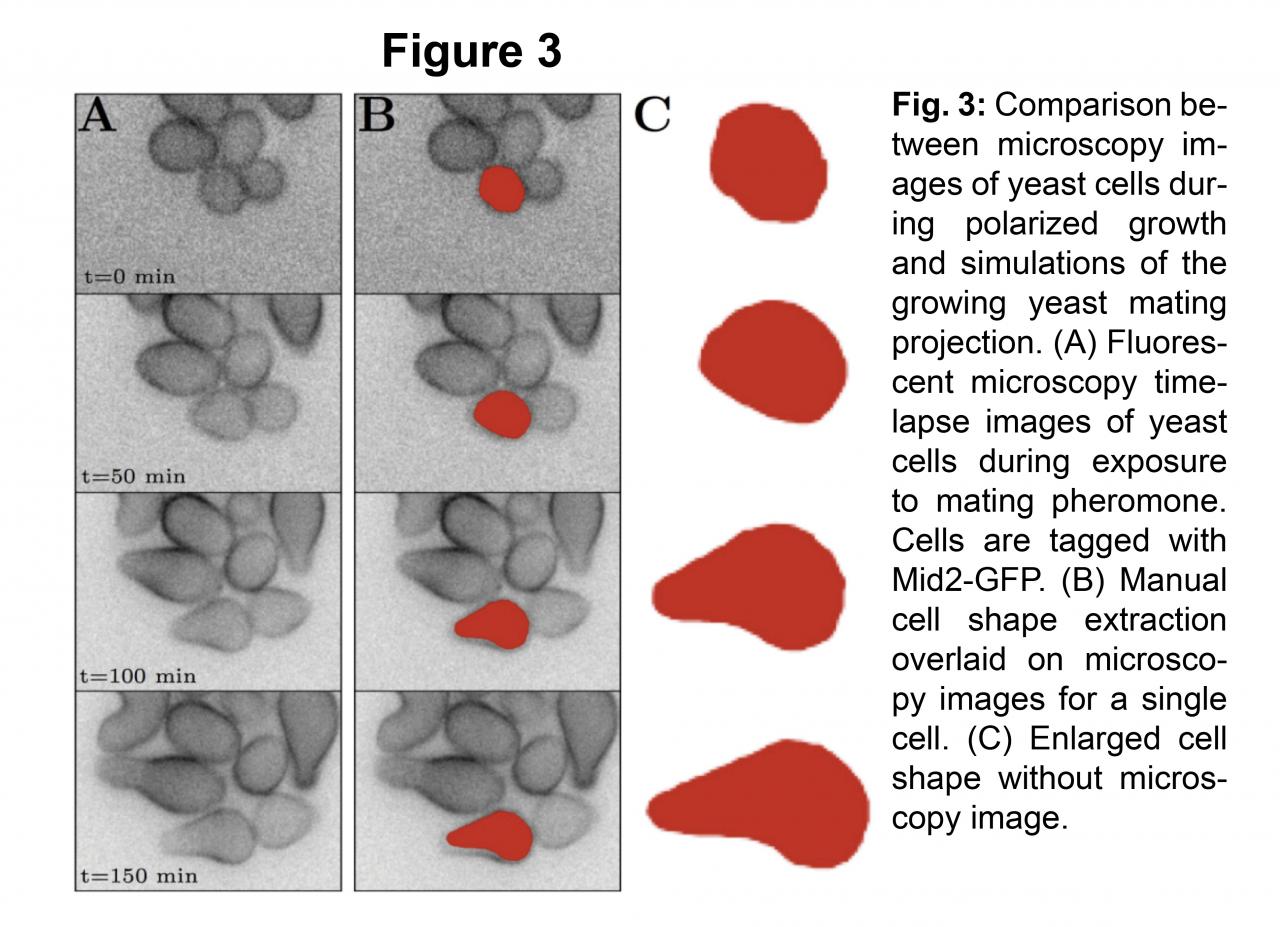
We have developed a computational framework to bridge the mechanics of cell wall expansion to intracellular dynamics using an operator splitting algorithm to couple spatial stochastic biochemical reactions to the slower mechanical dynamics associated with the cell wall. With this methodology, we have successfully simulated mating projection growth in a fully-coupled system driven by turgor pressure using a model of Cdc42 connected to the mechanics equations [2].

Despite the good results, we found that the coupling between a finite elements method and the stochastic algorithm resulted in technical difficulties with the meshing procedure. As a consequence, we have also explored a Lagrangian mess-free, particle-based approach. As a result, we developed a new algorithm merging discrete stochastic simulation, using the spatial stochastic simulation algorithm (sSSA), with the particle-based fluid dynamics simulation framework of smoothed dissipative particle dynamics (SDPD). This hybrid algorithm enables discrete stochastic simulation of spatially resolved chemically reacting systems on a mesh-free dynamic domain [3].

References

[1] Lawson MJ, Drawert B, Khammash M, Petzold L, Yi T-M. Spatial Stochastic Dynamics Enable Robust Cell Polarization. PLoS computational biology 9(7): e1003139, 2013.

[2] Samhita P Banavar, Carlos Gomez, Michael Trogdon, Linda R Petzold, Tau-Mu Yi, and Otger Campas. Mechanical feedback coordinates cell wall expansion and assembly in yeast mating morphogenesis. PLoS computational biology, 14(1):e1005940, 2018.

[3] Brian Drawert, Bruno Jacob, Zhen Li, Tau-Mu Yi, and Linda Petzold. A hybrid smoothed dissipative particle dynamics (SDPD) spatial stochastic simulation algorithm (sSSA) for advection–diffusion–reaction problems. Journal of Computational Physics, 378:1 – 17, 2019.