The aim of this work is to develop efficient and flexible methods for accurate modeling and simulation of intracellular biochemical processes, with target applications in biology [1] and medicine [2].
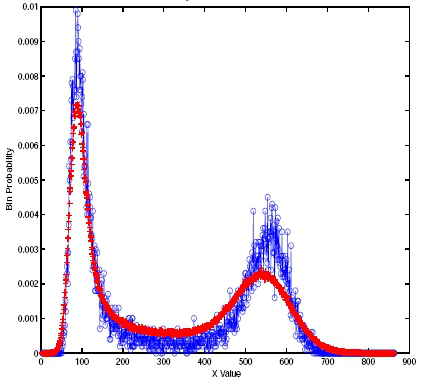
Histogram of the Schlögl model [7] based on 10,000 realizations of the SSA (blue) and explicit tau-leaping (red) methods. A deterministic simulation cannot capture the bistability of this model.
It has been established that traditional deterministic differential equation-based models may fail to capture important dynamics of biochemical systems due to the inherent randomness of the processes. The stochastic simulation algorithm (SSA) derived by Gillespie [3] faithfully captures the behavior of well-mixed systems by tracking the discrete copy number of each species and by simulating every reaction event.
In collaboration with Dan Gillespie, we have developed several multiscale stochastic simulation algorithms that take advantage of timescale separation of systems. Tau-leaping [4] is a method that allows larger time-steps by simulating multiple reactions in each time step. The slow-scale SSA (ssSSA) [5] accelerates simulations where fast reactions involve chemical species that are present in small numbers, and the slow-scale tau-leaping method [6] incorporates aspects of both the tau-leaping and ssSSA methods.
However, some systems do not satisfy the well-mixed condition, thus requiring a more detailed level of simulation. For such systems, spatial effects can be taken into account by either considering an extension of the SSA to a spatially heterogeneous setting (the next sub volume method (NSM) [8]), or even more fine-grained particle-tracking models.
Unfortunately, simulating systems with high spatial resolution is computationally intensive, and to make large computations feasible we are developing multiscale methods, taking advantage of separation of scales. Parts of a simulation can be carried out at a level with less spatial resolution, while other parts are carried out at a more fine-grained level [9].
|
Snapshot of a simulation using a modified version of the particle-tracking method Green's function reaction dynamics (GFRD) [10-12]. The motion of each particle is tracked. |
 Example of a spatial splitting. Molecules in the red region, that are close to the nucleus (green), are simulated at the microscopic level while molecules in the blue region, that are far from the nucleus, are simulated at the mesoscopic level. |
References
1. Lawson MJ, Drawert B, Khammash M, Petzold L, and Yi T-M (2013) Spatial Stochastic Dynamics Enable Robust Cell Polarization. PLoS Comput Biol 9(7): e1003139. doi:10.1371/journal.pcbi.1003139
2. Marc Sturrock, Andreas Hellander, Anastasios Matsavinos, and Mark Chaplain (2013) Spatial stochastic modeling of the Hes1 pathway: Intrinsic noise can explain heterogeneity in embryonic stem cell differentiation. J. Roy. Soc. Interface 10:20120988.
3. D.T Gillespie (1977) J. Phys. Chem. 81 (25): 2340-2361.doi:10.1021/j100540a008
4. Gillespie, D. T. (2001) Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115 (4): 1716-1711. doi:10.1063/1.1378322
5. Cao, Y., Gillespie, D. T., Petzold, L. R. (2005) The slow-scale stochastic simulation algorithm. J. Chem. Phys. 122(1):014116. doi: 10.1063/1.1824902
6. Cao, Y. and Petzold, L. (2008) Slow Scale Tau-leaping Method. Computer Methods in Applied Mechanics and Engineering 197:3472-3479.
7. Schlögl, F. and Berry R. S. (1980) Small roughness fluctuations in the layer between two phases. Phys. Rev. A, 21(6):2078-2081.
8. Elf and Ehrenberg (2004) Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst. Biol. 1(2):230-236. doi:10.1049/sb:20045021
9. Andreas Hellander, Stefan Hellander and Per Lötstedt (2012) Coupled mesoscopic and microscopic simulation of stochastic reaction-diffusion processes in mixed dimensions. Multiscale Model. Simul. 10(2):585-611.
10. Van Zon JS, Ten Wolde PR (2005) Simulating biochemical networks at the particle level in time and space: Green's Function Reaction Dynamics.Phys Rev Lett, 94: 128103.
11. S. Hellander and P. Lötstedt. (2011) Flexible Single Molecule Simulation of Reaction-Diffusion Processes. J. Comput. Phys., 230(10):3948-3965.
12. Hellander, S. (2012) Single molecule simulations in complex geometries with embedded dynamic one-dimensional structures. J. Chem. Phys., 130(1):014103.
